PyTorchで学ぶディープラーニング：はじめてのニューラルネットワーク構築

はじめに

この記事では、ディープラーニングフレームワークの1つである PyTorchを使って、
初めてのニューラルネットワークを構築してみましょう

PyTorchとは？

PyTorchとは、オープンソースの機械学習フレームワークで、主にディープラーニングのアプリケーションを開発するために使用されます
FacebookのAIリサーチグループによって開発され、Pythonプログラミング言語で書かれています
PyTorchは、ニューラルネットワークの設計、トレーニング、および評価を容易にする、
柔軟で直感的なインターフェースを提供します
この記事では、PyTorchを使って、基本的なニューラルネットワークを構築し、学習を行います

PyTorchの特徴

PyTorchの主な特徴は以下の通りです

1. 動的計算グラフ (Dynamic Computation Graph)
   計算グラフを動的に構築し、実行時に変更できるため、デバッグが容易であり、
   柔軟なモデルアーキテクチャを実現できます
2. 自動微分 (Automatic Differentiati)
   モデルの勾配を計算するための自動微分機能を備えており、誤差逆伝播（バックプロパゲーション）の実装が簡単です
3. GPUアクセラレーション
   NVIDIAのCUDAおよびcuDNNライブラリを活用し、高速なGPUを使って
   ディープラーニングの計算を行うことができます
   AppleのM1/M2のGPUにも対応しています
4. 分散学習と複数GPUサポート
   分散学習と複数のGPUを使用したモデルトレーニングをサポートしており、大規模なデータセットや複雑なモデルに対応できます
5. モデルの保存と読み込み
   学習したモデルの重みやパラメータを、簡単に保存および読み込むことができ、
   再利用やデプロイが容易です

PyTorchの基礎

PyTorchは

問題設定

分類問題をニューラルネットワークで解いてみたいと思います
分類問題がわからない方は下記記事を見てみてください

分類問題の概念

１０分でわかる教師あり学習の概念

今回は２つの特徴量で３つのクラスに分割する問題を考えます
下記画像のような状況です
特徴量２つは 例えば、身長と体重のペアや費用と時間のペアなどがあります

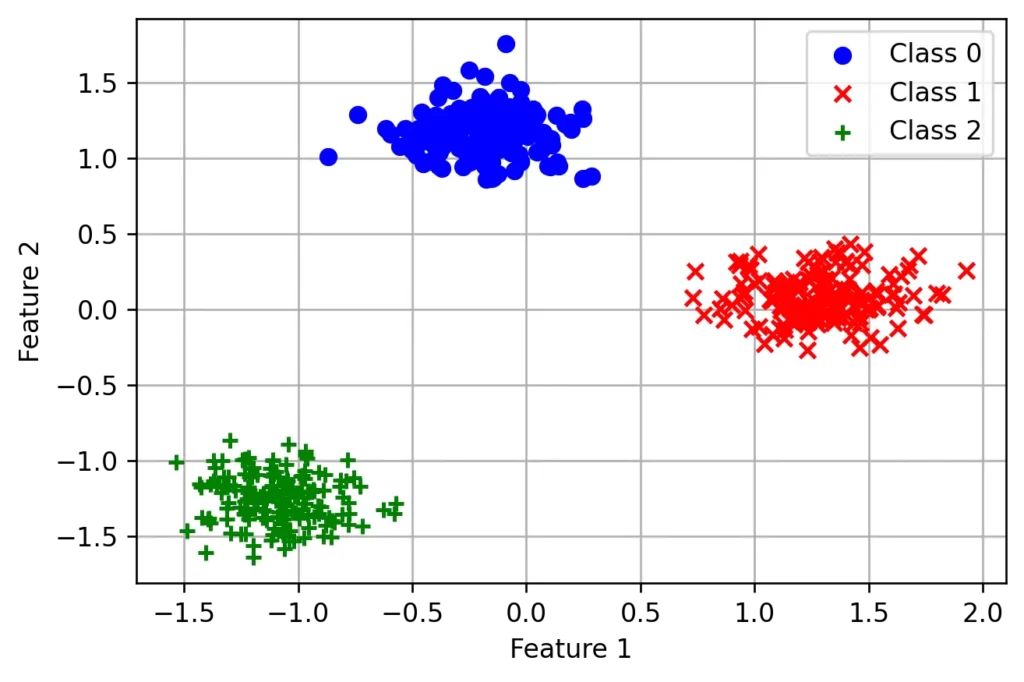
この３つのクラスを分類する予測モデルを作ることがゴールとなります
具体的には、下記の図のように黄色のデータが与えられた時に、どこのクラスに属しているかを予測するモデルです

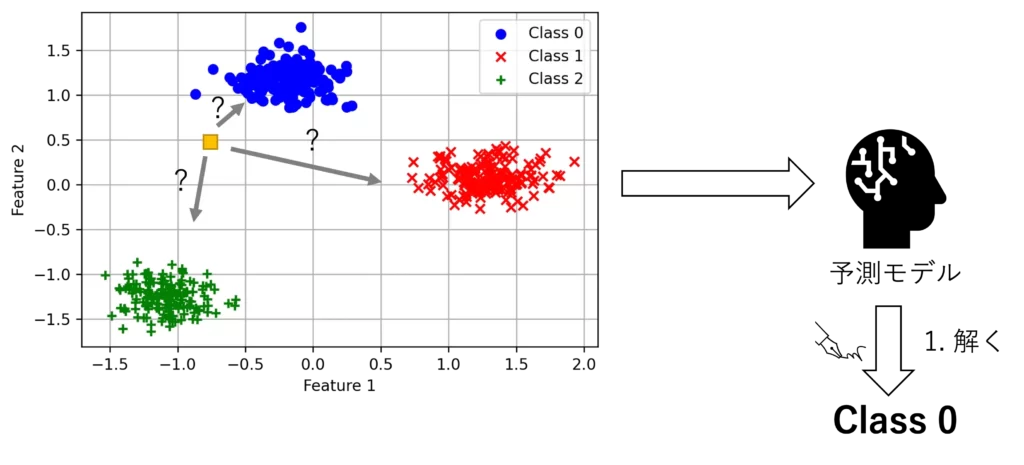
データ生成

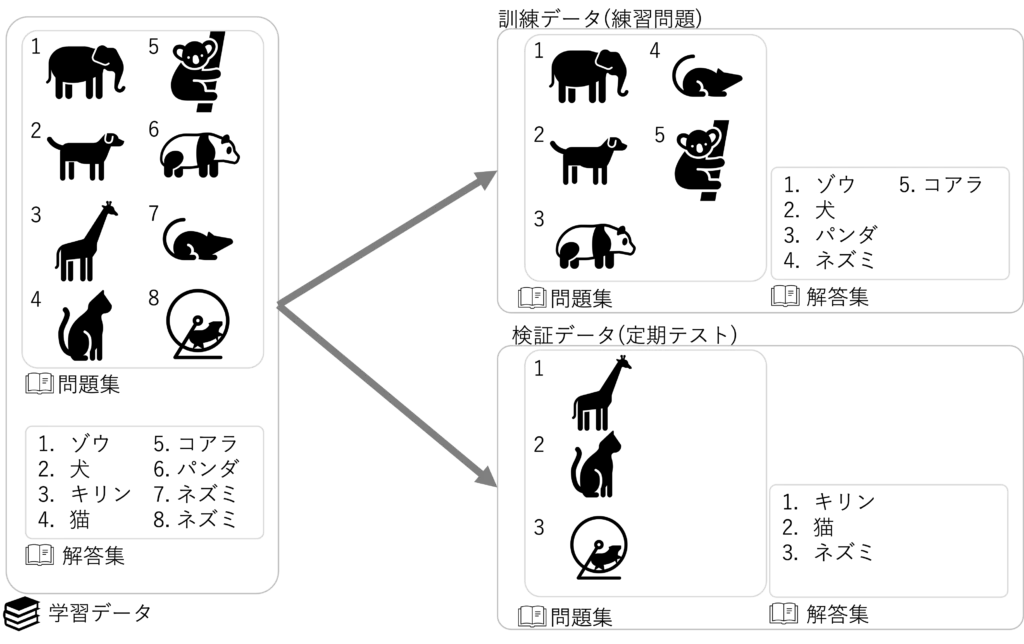
まず学習に必要な、３つに分類できる500個の学習データを作ってみます
機械学習の枠組みの赤点線の部分になります
具体的には下記のPythonコードになります

# 必要なライブラリのインポート
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

class_num = 3
feature_num = 2

# データの生成
data, labels = make_blobs(n_samples=500,
                          centers=class_num,
                          n_features=feature_num,
                          random_state=42)
data = StandardScaler().fit_transform(data)

# データの分割
train_data, val_data, train_labels, val_labels = train_test_split(data, labels,
                                                              test_size=0.2,
                                                              random_state=42)

# numpy配列をPyTorchのテンソルに変換
train_data = torch.tensor(train_data, dtype=torch.float32)
train_labels = torch.tensor(train_labels, dtype=torch.long)
val_data = torch.tensor(val_data, dtype=torch.float32)
val_labels = torch.tensor(val_labels, dtype=torch.long)

ひとつずつコードを見ていきます

最初部分のfrom...から続く３行は、scikit-learnという機械学習用のライブラリの中にある
モジュールを読み込んでます
今回は学習データの生成に使っています
具体的なモジュールの内容はこの後で説明していきます

次に出てくるclass_numは分類数を表しています
今回は、３としたので、3つに分類されることになります

feature_numは次元数を表しています
今回は２次元ですが、feature_numを３にすれば、３次元のデータが得られます。

データの生成ブロックを見ていきます
data, labels = make_blobs(...) はデータを生成する関数です

返り値のdataは、上の図の問題集、labelは解答集になります
引数についてですが、n_samplesは出力するデータ数、centersは分類数、
n_featuresは次元数、random_stateは乱数の種（シード）というものになります
特にrandom_stateは、関数の挙動を再現可能にするために設定されます
つまり、同じシード値を指定することで、何度実行しても同じデータが生成されるようになります

data = StandardScaler().fit_transform(data) はデータの標準化を行なっています
標準化は、特徴量のスケールを揃えるために行われる前処理の一種で、データの平均を0、
標準偏差を1に変換します

train_data, val_data, train_labels, val_labels = train_test_split()は、学習データを訓練データと検証データに分離しています
train_data, val_data, train_labels, val_labelsは、それぞれ訓練データ、
検証データ、訓練データのラベル(解答集)、検証データのラベル（解答集）になります

引数ですが、元々の学習データ(data)とラベル(label)、検証データの割合(test_size)、
訓練データと検証データを分ける際の乱数の種(random_state)になります
データをシャッフルするので乱数が必要になってきます

最後のブロックは、PyTorchでデータを扱うので numpyの配列からPyTorchのテンソル型に変換を行なっています

ニューラルネットワークの構築

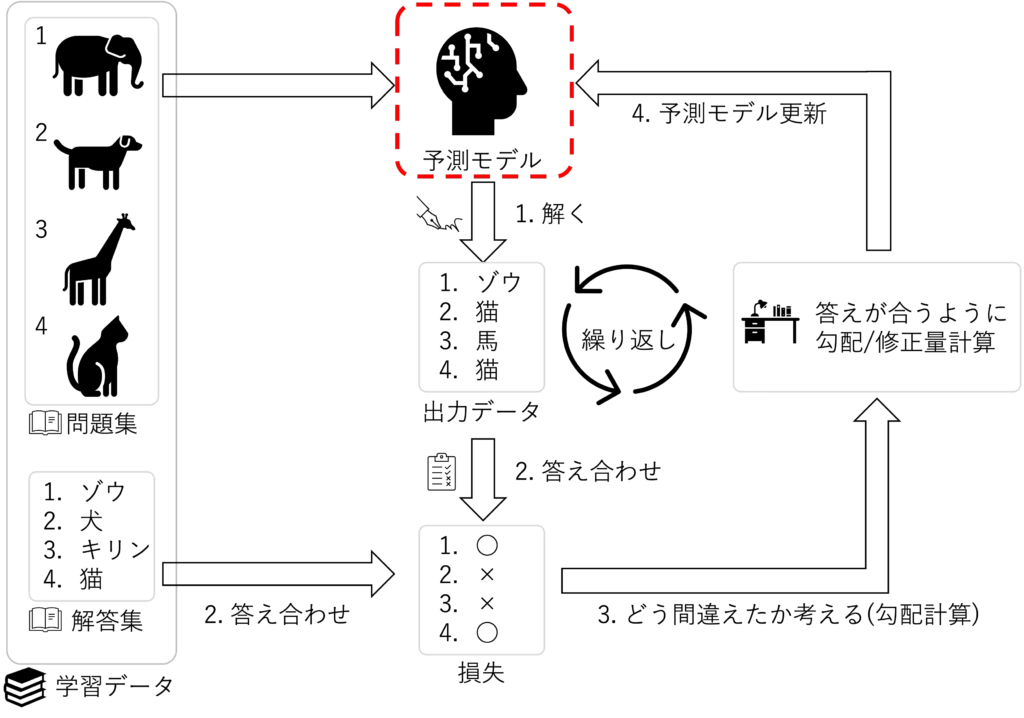
次に予測モデル、上図の赤線の部分を実装していきます
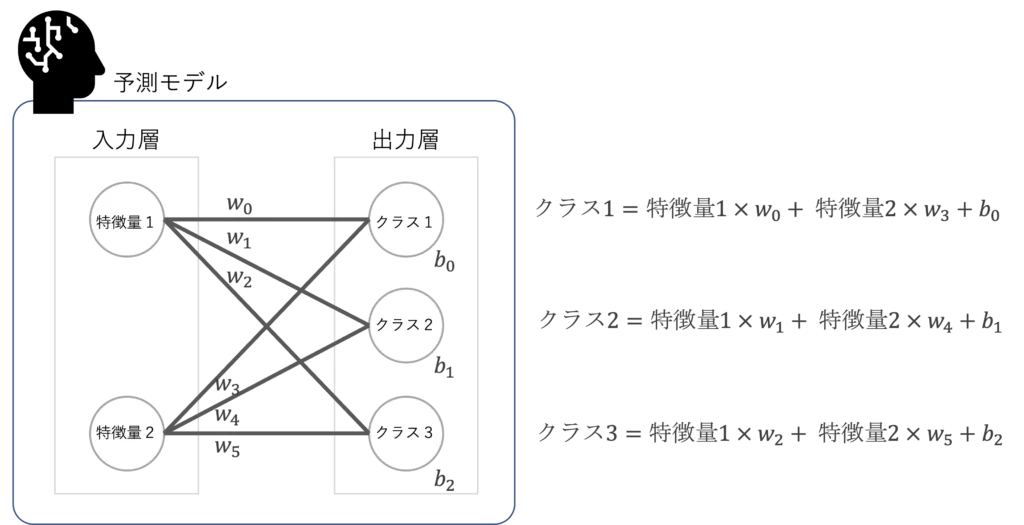
ここでは、入力層と出力層の全結合層からなるニューラルネットワークを作成します
具体的には、下のコードになります

# モデルの定義
class SimpleClassifier(nn.Module):
    def __init__(self, input_size, output_size):
        super(SimpleClassifier, self).__init__()
        self.fc = nn.Linear(input_size, output_size)

    def forward(self, x):
        return self.fc(x)

nn.Moduleは、PyTorchにおけるニューラルネットワークのモジュール（レイヤー）すべてのベースとなるクラスです
このモデルの書き方が、PyTorchでは基本になります
入力サイズ（input_size）と出力サイズ（output_size）を引数に取り、
全結合層（nn.Linear）を作成しています。全結合層は、入力と出力のサイズに基づいて
線形変換を行う層です
入力層と出力層だけの単純なニューラルネットワークになります
下図の\(w_i\)は重み(weight)、\(b_i\)はバイアス(bias)と呼ばれる変数です

学習時に、これらの変数を最適化していくことになります
(具体的には、学習を繰り返しながら 最も正解に近くなる時のweight と bias を求めることです)

学習ループ

最後に学習ループ部分の実装になります

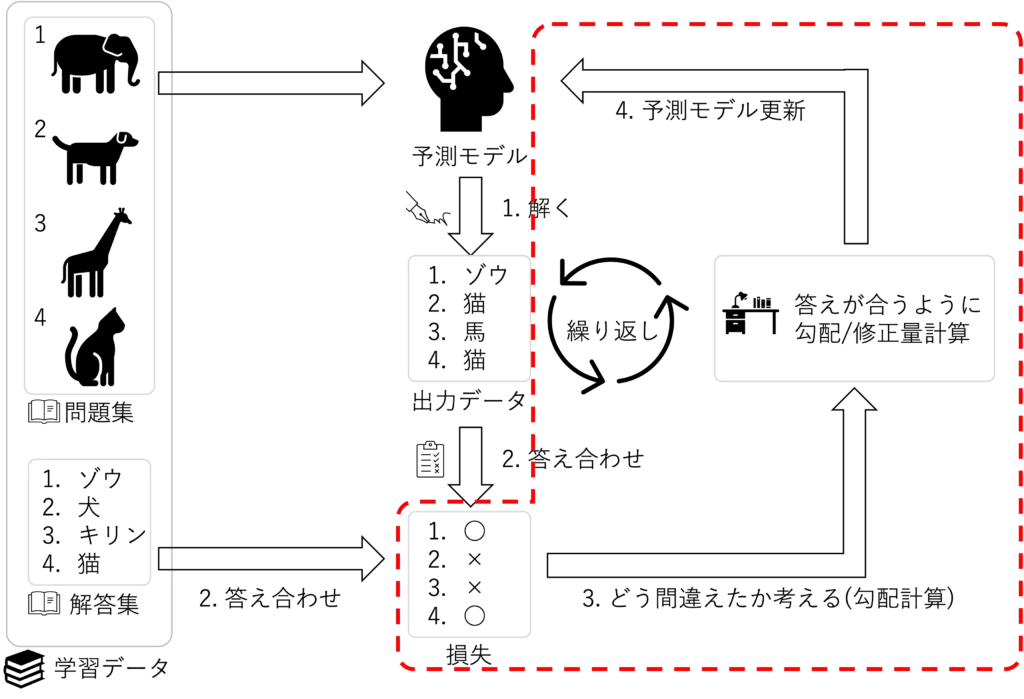
コードの実装は下記のようになります

# ハイパーパラメータ
num_epochs = 1000
learning_rate = 0.01

# モデル、損失関数、オプティマイザの定義
input_size = feature_num
output_size = class_num
model = SimpleClassifier(input_size, output_size)
loss_function = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=learning_rate)

# 学習
for epoch in range(num_epochs):
    # オプティマイザの勾配初期化
    optimizer.zero_grad()
    # 予測モデルが問題を解く
    predictions = model(train_data)
    # 答え合わせしてどれくらい間違えているかを確認
    loss = loss_function(predictions, train_labels)
    # どう間違えたかを考える(勾配計算)
    loss.backward()
    # 予測モデルを更新
    optimizer.step()

    if (epoch + 1) % 100 == 0:
        print(f"Epoch: {epoch + 1}, Loss: {loss.item():.4f}")

一番最初のハイパーパラメータの設定は、学習の回数と学習率の設定を行なっています
学習率とは、一回の学習で どれくらいモデルのパラメータを更新するかという値になります
大きく設定すると早く学習（収束）するかもしれませんが、学習の過程でモデルが安定しない（発散）リスクがあります
一般的に小さな値を設定して時間をかけて学習を行います

次にモデル、損失関数、オプティマイザの定義の部分の説明をします
モデルは、先ほどのコードで定義したニューラルネットワークの予測モデルになります

損失関数は、予測モデルと解答集を比べて、どれくらい間違えているかを計算する関数です
今回は分類問題なので、最後に予測値を確率にする必要があります
そこで、クロスエントロピーという損失関数を採用しています

最後のオプティマイザは、モデルを修正する時の修正方向を計算する関数になります
入力引数としては予測モデルのパラメータと学習率になります

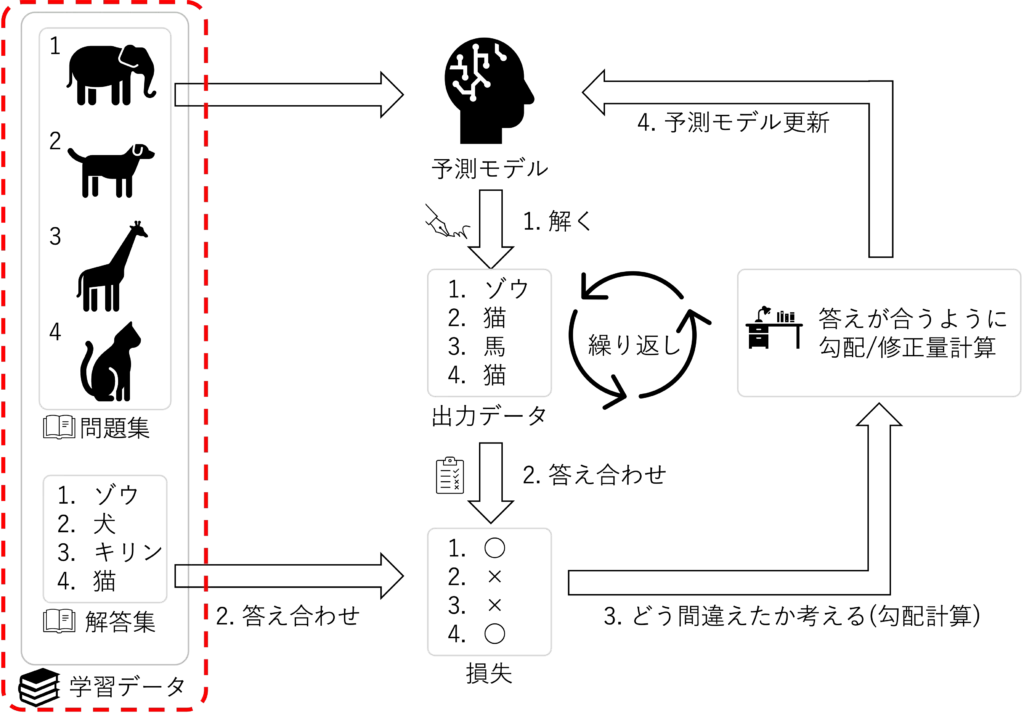
最後の学習ブロックは、上図の繰り返しを実行しています
optimizer.zero_grad()：オプティマイザの勾配値を初期化しています
オプティマイザは勾配の計算をし続けるので、必要に応じて初期化して、勾配計算をしないということを明示的に書く必要があります

predictions = model(train_data)：予測モデルに訓練データを入力して予測値を出力

loss = loss_function(predictions, train_labels)：答え合わせの結果、どのくらい正解とずれているのかを計算
予測モデルで出力された予測値と訓練データの解答集を比べて、答え合わせを行なっています

loss.backward()：どう修正すればいいか考える
どう修正すればいいかを計算するために、間違いの方向（勾配）を計算しています

optimizer.step()：モデルの修正を行います

最後は100回ごとに学習の内容を確認するために、print文で出力を行なっています出力は下記のようになります
学習回数を重ねるごとに損失が減っていることが確認できます
Epoch: 100, Loss: 0.5763
Epoch: 200, Loss: 0.3788
Epoch: 300, Loss: 0.2797
Epoch: 400, Loss: 0.2213
Epoch: 500, Loss: 0.1831
Epoch: 600, Loss: 0.1561
Epoch: 700, Loss: 0.1362
Epoch: 800, Loss: 0.1208
Epoch: 900, Loss: 0.1086
Epoch: 1000, Loss: 0.0986

検証

最後に学習モデルを未知のデータ(検証用データ)で検証を行ってみましょう

# 検証データで評価
with torch.no_grad():
    val_predictions = model(val_data)
    val_loss = loss_function(val_predictions, val_labels)

    _, predicted_labels = torch.max(val_predictions, 1)
    correct = (predicted_labels == val_labels).sum().item()
    accuracy = correct / len(val_labels)

    print(f"Validation Loss: {val_loss.item():.4f}, Accuracy: {accuracy:.4f}")

検証では、学習で使っていない検証用データで予測モデルの精度を評価します
最初のwith torch.no_grad():ですが今回は学習は行わないので、勾配の計算は不要です
勾配を計算しないことを表しています

val_predictions = model(val_data),
val_loss = loss_function(val_predictions, val_labels)：は、検証データを学習済み予測モデルに入れた時の予測値および損失値を計算しています

_, predicted_labels = torch.max(val_predictions, 1)：予測値の抽出
torch.max関数は、テンソル（配列）の最大値とそのインデックスを返す関数です
val_predictionsの中で最も値が高いものが予測クラスになるので、それを抽出します

correct = (predicted_labels == val_labels).sum().item()：正解数を数える
予測値と正解値が一致している数の合計値を計算しています

accuracy = correct / len(val_labels)：精度の計算
正解数/全体数を計算することで、精度の計算を行ってます

出力は下記のようになります
Validation Loss: 0.0917, Accuracy: 1.0000
学習時に使っていない検証データにおいても高い精度であることが確認できます

まとめ

今回はPyTorchを使った簡単な分類の問題を解きました
画像分類や複雑な回帰問題も同様のフレームワークで実装をしていきます

ラーニングマン

エンジニアサラリーマン

仕事で使いそうだから機械学習を色々勉強しましたが、あまり使わなかった中堅エンジニアです。

せっかくなので、これから機械学習・ディープラーニングを勉強しようと思っている人の助けになればと思いブログを立ち上げました。

間違いやアドバイスがあれば気軽に連絡していただけると嬉しいです。